|
課程設計報告 課程名稱:《通信系統原理》 系別:通信工程系 學生姓名: 班級:1988通信(2)班 學號: 成 績: 指導教師: 開課時間:2017-2018學年第一學期
引言數字基帶傳輸系統用來傳輸未經載波調制的基帶信號,在某些具有低通特性的有線信道中,特別是在傳輸距離不太遠的情形下應用較為廣泛。是一種不搬移基帶信號頻譜的傳輸方式。 選用基帶傳輸或通帶傳輸,與信道的適用頻帶有關。未對載波調制的待傳信號稱為基帶信號,它所占的頻帶稱為基帶,基帶的高限頻率與低限頻率之比通常遠大于1。 基帶傳輸中的碼型變換裝置把來自信源的數碼變換為適合于信道傳輸的碼波形。常用的傳輸碼波形有歸零碼、不歸零碼、傳號差分碼、雙相碼、交替傳號反轉碼(AMI碼)等。 基帶傳輸廣泛用于音頻電纜和同軸電纜等傳送數字電話信號,同時,在數據傳輸方面的應用也日益擴大。通帶傳輸系統中調制前和調制后對基帶信號處理仍須利用基帶傳輸原理,采用線性調制的通帶傳輸系統可以變換為等效基帶傳輸來分析。
課程設計目的
本課程是為通信工程專業本科生開設的必修課,結合學生的專業方向的理論課程,充分發揮學生的主動性,使學生掌握應用MATLAB或者SYSTEMVIEW等仿真軟件建立通信系統,鞏固理論課程內容,規范文檔的建立,培養學生的創新能力,并能夠運用其所學知識進行綜合的設計。 通信系統原理的課程設計是對通信系統仿真軟件、課程學習的綜合檢驗,配合理論課的教學,讓學生親自參加設計、仿真、驗證通信系統的一般原理、調制解調原理、信號傳輸及受噪聲影響等方面的知識點。
目錄 一、設計題目 二、主要內容 三、具體要求 四、進度安排 五、成績評定 六、數字基帶傳輸系統基本原理 6.1數字基帶系統模型 6.2數字基帶傳輸系統原理 七、數字基帶系統波形及碼型 7.1 四種常見波形的原理 7.1.1單極性歸零波形 7.1.2單極性非歸零波形 7.1.3雙極性歸零波形 7.1.4 雙極性非歸零波形 7.2基帶信號的常用碼型 7.2.1 AMI碼(傳號交替反轉碼) 7.2.2 HDB3碼(三階高密度雙極性碼) 7.2.3曼徹斯特碼(雙相碼) 7.2.4密勒碼(Miller碼) 7.3升余弦滾降濾波器 7.4 眼圖 八、MATLAB 仿真及程序調制 8.1單極性歸零波形 8.2單極性非歸零波形 8.3雙極性歸零波形 8.4雙極性非歸零波形 8.5AMI碼 8.6HDB3碼 8.7曼徹斯特碼 8.8Miller 九、心得體會 十、參考文獻
一、設計題目數字基帶傳輸系統的仿真設計(常見的波形與碼型設計)
二、主要內容(1)數字基帶傳輸系統,理想信道和非理想信道的系統設計; (2)設計基帶信號的常見波形; (3)設計基帶信號的常用碼型; (4)眼圖。
三、具體要求(1)熟悉基帶傳輸系統的基本結構。可利用matlab和simulink對數字基帶傳輸系統進行設計和仿真,實現數字基帶傳輸系統設計。 (2)設計基帶信號的常見波形。給出基帶信號的常見波形(單極性歸零碼、不歸零碼,雙極性歸零碼、不歸零碼) 等。 (3)設計基帶信號的常用碼型;設計出碼型(AMI、HDB3碼、雙相碼、密勒碼等)設計。(注:碼型設計不少于四種) (4)眼圖。盡可能給出性能評價:通過觀測眼圖,定性判斷數字基帶傳輸系統的性能(加分項)。
四、進度安排星期二 選題、查閱資料、熟悉軟件的編程環境MATLAB/SIMULINK并結合推薦的參考書,熟悉對應的模塊。 星期三 數字基帶信號常見的波形。 星期四 數字基帶信號常見的碼型設計(AMI碼、HDB3碼)。 星期五 數字基帶傳輸系統的仿真設計(今日應該做到:數字基帶信號常見的碼型設計(雙相碼、密勒碼));程序調試并程序注釋。
五、成績評定總成績由平時成績(考勤與課堂表現)、程序設計成績和報告成績三部分組成,各部分比例為30%,50%,20%. (1)平時成績:無故曠課一次,平時成績減半;無故曠課兩次平時成績為0分,無故曠課三次總成績為0分。遲到15分鐘按曠課處理 (2)設計成績:按照實際的設計過程及最終的實現結果給出相應的成績。 (3)設計報告成績:按照提交報告的質量給出相應的成績。
六、數字基帶傳輸系統基本原理6.1數字基帶系統模型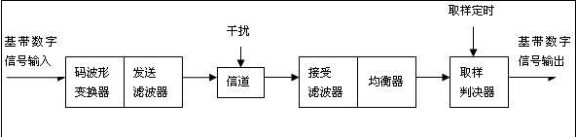
圖6.1基帶傳輸系統模型 (1)信道信號形成器(發送濾波器)。它的功能是產生適合于信道傳輸的基帶信號波形。因為其輸入一般是經過碼型編碼產生的傳輸碼,相應的基本波形通常是矩形脈沖,其頻譜很寬,不利于傳輸。發送濾波器用于壓縮輸入信號頻帶,把傳輸碼變成適宜于信道傳輸的基帶信號波形。 (2)信道。是允許基帶信號通過的媒質,通常為有線信道,如雙絞線、同軸電纜等。信道的傳輸特性一般不滿足無失真傳輸條件,因此也會引起傳輸波形的失真。另外信道還會引入噪聲n(t),并假設它是均值為零的高斯白噪聲。 (3)接收濾波器。它用來接收信號,盡可能濾除信道噪聲和其他干擾,對信道特性進行均衡,使輸出的基帶波形有利于抽樣判決。 (4)抽樣判決器。則是在傳輸特性不理想及噪聲背景下,在規定時刻(由定位時脈沖控制)對接收濾波器的輸出波形進行抽樣判決,以恢復或再生基帶信號。 (5)定時脈沖和同步提取。用來抽樣的位定時脈沖依靠同步提取電路從接收信號中提取,位定時的準確與否將直接影響判決效果。 6.2數字基帶傳輸系統原理假設輸入符號序列為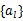 ,在二進制的情況下,符號 ,在二進制的情況下,符號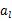 的取值為0,1或-1,+1。為方便分析,我們把這個序列對應的基帶信號表示成 的取值為0,1或-1,+1。為方便分析,我們把這個序列對應的基帶信號表示成 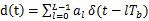 這個信號是由時間間隔為Tb的單位沖激響應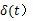 構成的序列,其每一個 構成的序列,其每一個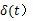 強度則由 強度則由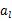 決定。 決定。 離散域發送信號——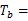 A A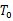 ,比特周期,二進制碼元周期 ,比特周期,二進制碼元周期 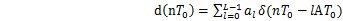
設發送濾波器的傳輸特性  或 或 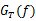 則 則 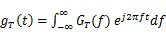
當 激勵發送濾波器時,發送濾波器產生的輸出信號為 激勵發送濾波器時,發送濾波器產生的輸出信號為  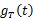 = =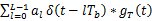 = =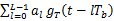
離散域發送濾波器輸出: 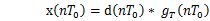 = =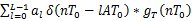 = =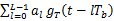
信道輸出信號 (信道特性為1) (信道特性為1) 離散域信道輸出信號或接收濾波器輸入信號——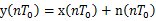 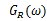 或 或  或 或 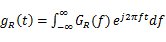
則接收濾波器的輸出信號  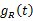 = =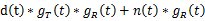
=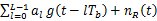 其中 其中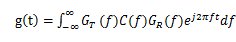 離散域接收濾波器的輸出信號 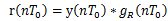 = =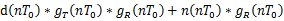
=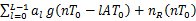 其中g(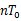 )= )=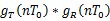 如果位同步理想,則抽樣時刻為 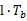 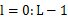 抽樣點數值為 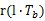 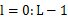 判決為 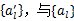 比較即可得到誤碼率,分析傳輸質量。 比較即可得到誤碼率,分析傳輸質量。 七、數字基帶系統波形及碼型
7.1 四種常見波形的原理
7.1.1單極性歸零波形單極性歸零碼(RZ)即是以高電平和零電平分別表示二進制碼1 和0,而且在發送碼1 時高電平在整個碼元期間T 只持續一段時間τ,其余時間返回零電平.在單極性歸零碼中,τ/T 稱為占空比.單極性歸零碼的主要優點是可以直接提取同步信號,因此單極性歸零碼常常用作其他碼型提取同步信號時的過渡碼型.也就是說其他適合信道傳輸但不能直接提取同步信號的碼型,可先變換為單極性歸零碼,然后再提取同步信號. 當發“1”碼時,發出正電流,但持續時間短于一個碼元的時間寬度,即發出一個窄脈沖;當發出“0”碼時,仍然不發送電流。 7.1.2單極性非歸零波形單極性非歸零碼(NRZ)是一種與單極性歸零碼相似的二元碼,但碼脈沖之間無間隔,這是一種最常見的碼型。單極性非歸零碼的特點是:有直流成分,因此很難在低頻傳輸特性比較差的有限信道進行傳輸,并且接收單極性非歸零碼的判決電平一般取為1碼電平的一半,因此在信道特性發生變化時,容易導致接收波形的振幅和寬度變化,使得判決電平不能穩定在最佳電平,從而引起噪聲,此外,單極性不歸路碼還不能直接提取同步信號,并且傳輸時必須將信道一端接地,從而對傳輸線路有一定要求,一般由終端送來的單極性非歸零碼要通過碼型變換變成適合信道傳輸的碼型。 無電壓表示“0”時,恒定正電壓表示“1”,每個碼元時間的中間點是采樣時間,判決門限為半幅電平。 7.1.3雙極性歸零波形雙極性歸零碼是二進制碼0 和1 分別對應于正和負電平的波形的編碼,在每個碼之間都有間隙產生.這種碼既具有雙極性特性,又具有歸零的特性.雙極性歸零碼的特點是:接收端根據接收波形歸于零電平就可以判決1 比特的信息已接收完畢,然后準備下一比特信息的接收,因此發送端不必按一定的周期發送信息.可以認為正負脈沖的前沿起了起動信號的作用,后沿起了終止信號的作用.因此可以經常保持正確的比特同步.即收發之間無需特別的定時,且各符號獨立地構成起止方式,此方式也叫做自同步方式.由于這一特性,雙極性歸零碼的應用十分廣泛。 其中“1”碼發生正的窄脈沖,“0”碼發出負的窄脈沖,兩個碼元的時間間隔可以大于每一個窄脈沖的寬度,取樣時間是對準脈沖的中心。 7.1.4 雙極性非歸零波形雙極性非歸零碼是用正電平和負電平分別表示二進制1和0的碼型,它與雙極性歸零碼類似,但雙極性非歸零碼的波形在整個碼元持續期間電平保持不變,雙極性非歸零碼的特點是:從統計平均來看,該碼型信號在1和0的數目各占一半時無直流分量,并且接收時判決電平為0,容易設置并且穩定,因此抗干擾能力強。此外,可以在電纜等無接地的傳輸線上傳輸,因此雙極性非歸零碼應用極廣。雙極性非歸零碼中提取同步信號,并且1碼和0碼不等概時,仍有直流成分。 “1”碼和“0”碼都有電流,“1”為正電流,“0”為負電流,正和負的幅度相等,判決門限為零電平。 7.2基帶信號的常用碼型
7.2.1 AMI碼(傳號交替反轉碼)編碼規則:“0”碼不變,“1”碼則交替地轉換為+1和-1。當碼序列是1 0 0 1 0 0 0 1 1 1 0 1時,AMI碼就變為:+1 0 0 -1 0 0 0 +1 -1 +1 0 -1。這種碼型交替出現正、負極脈沖,所以沒直流分量,低頻分量也很少。這種碼的反變換也很容易,在再生信碼時,只要將信號整流,即可將“-1”翻轉為“+1”,恢復成單極性碼。這種碼未能解決信碼中經常出現的長連“0”的。 7.2.2 HDB3碼(三階高密度雙極性碼)a、編碼規則: ①1——交替變換為+1,-1。 ②0——連0小于等于3,則用0電平表示,連0大于3,則用特定碼組替換B 0 0 V或 0 0 0 V。 ③任意兩個V之間B的個數為奇數。 b、特點:①有檢錯能力 ②解決了連“0”時位定時信息提取困難 ③無直流分量 ④B碼和V碼各自保持極性交替變化,以確保無直流分量 ⑤可能存在誤碼擴散的問題 c、解碼規則:尋找兩個相鄰的同極性碼,后者即為“V”碼;把“V”碼連同其前3位碼均改為“0”, 所有的“±1”均改為“1”,即恢復信號。 7.2.3曼徹斯特碼(雙相碼)編碼規則:在信號位中電平從高到低跳變表示1;在信號位中電平從低到高跳變表示0;差分曼徹斯特編碼的編碼規則是:在信號位開始時不改變信號極性,表示輯"1",在信號位開始時改變信號極性,表示邏輯"0",不論碼元是1或者0,在每個碼元正中間的時刻,一定有一次電平轉換。 7.2.4密勒碼(Miller碼)密勒碼也稱延遲調制碼,是一種變形雙向碼。其編碼規則:對原始符號"1"碼元起始不躍變,中心點出現躍變來表示,即用10或01表示。對原始符號"0"則分成單個"0"還是連續"0"予以不同處理;單個"0"時,保持0前的電平不變,即在碼元邊界處電平不躍變,在碼元中間點電平也不躍變;對于連續"0",則使連續兩個"0"的邊界處發生電平躍變。 密勒碼可由雙相碼的下降沿去觸發雙穩電路產生。密勒碼最初用于氣象衛星和磁記錄,現在也用于低速基帶數傳機。 7.3升余弦滾降濾波器①理想低通特性 H(t)=Sa[π/Ts]←→H(W)=TsRet(W/WS) Sa(πt/T) 信號帶寬最小的波形
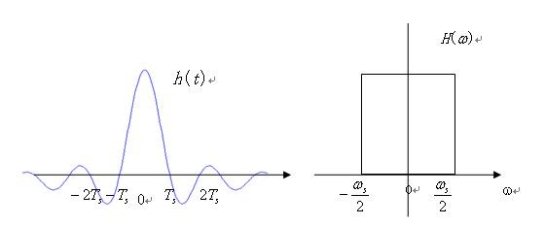 圖7.3.1濾波器的波形及頻域特性 理想低通信號的主要缺點 a.工程上難以實現; b.尾部衰減慢(沖激響應h(t)波形收斂速度較慢,拖尾以1/t速率衰減,當存在定時誤差時會帶來比較大的干擾) ②升余弦滾降特性:H(t)=Sa(πt/Ts)cos(aπt/Ts)/[(1-4aatt)/Ts] H(w)=Ts ;∣w∣< π/Ts(1-a) H(w)=0 ;∣w∣> π/Ts(1-a) 升余弦滾降信號的波形與頻譜: 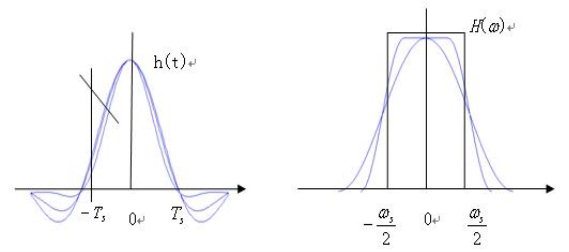
圖7.3.2 升余弦滾降信號的波形及頻譜 傳輸寬帶:B=(1+a)/2rs 頻帶利用率:g=rs/B=2/(1+a) 全升余弦系統:a=1 7.4 眼圖眼圖是指利用實驗的方法估計和改善(通過調整)傳輸系統性能時在示波器上觀察到的一種圖形。觀察眼圖的方法是:用一個示波器跨接在接收濾波器的輸出端,然后調整示波器掃描周期,使示波器水平掃描周期與接收碼元的周期同步,這時示波器屏幕上看到的圖形像人的眼睛,故稱 為 “眼圖”。從“眼圖”上可 以觀察出碼間串擾和噪聲的影響,從而估計系統優劣程度。另外也可以用此圖形對接收濾波器的特性加以調整,以減小碼間串擾和改善系統的傳輸性能。眼圖 的 “眼睛” 張開的大小反映著碼間串擾的強弱。 “眼睛”張的 越大,且眼圖越端正,表示碼間串擾越小;反之表示碼間串擾越大。當存在噪聲時,噪聲將疊加在信號上,觀察到的眼圖的線跡會變得模糊不清。若同時存在碼間串擾 ,“眼睛”將 張開得更小。與無碼間串擾時的眼圖相比,原來清晰端正的細線跡,變成了比較模糊的帶狀線,而且不很端正。噪聲越大,線跡越寬,越模糊;碼間串擾越大,眼圖越不端正。眼圖對于展示數字信號傳輸系統的性能提供了很多有用的信息:可以從中看出碼間串擾的大小和噪聲的強弱,有助于直觀地了解碼間串擾和噪聲的影響,評價一個基帶系統的性能優劣;可以指示接收濾波器的調整,以減小碼間串擾。 (1)最佳抽樣時刻應在“眼睛” 張開最大的時刻。 (2)對定時誤差的靈敏度可由眼圖斜邊的斜率決定。斜率越大,對定時誤差就越靈敏。 (3)在抽樣時刻上,眼圖上下兩分支陰影區的垂直高度,表示最大信號畸變。 (4)眼圖中央的橫軸位置應對應判決門限電平。 (5)在抽樣時刻上,上下兩分支離門限最近的一根線跡至門限的距離表示各相應電平的噪聲容限,噪聲瞬時值超過它就可能發生錯誤判決。 (6)對于利用信號過零點取平均來得到定時信息的接收系統,眼圖傾斜分支與橫軸相交的區域的大小,表示零點位置的變動范圍,這個變動范圍的大小對提取定時信息有重要的影響。
眼圖
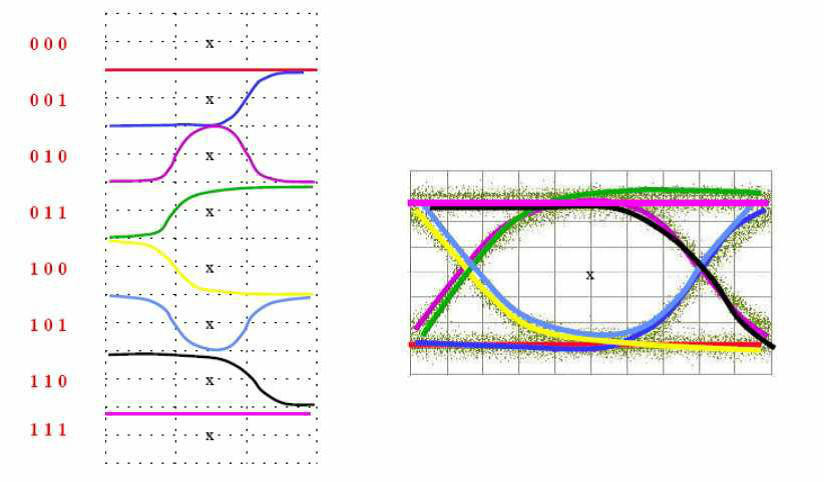
圖7.4眼圖 八、MATLAB 仿真及程序調制
8.1單極性歸零波形- function y = srz(x)
- x=[1 0 1 0 1 1 0 0 0 1 0 1]
- grid=200;
- t=0:1/grid:length(x);
- for i=1:length(x);
- if (x(i)==1)
- for j=1:grid/2
- y(grid/2*(2*i-1)+j)=1;
- y(grid/2*(2*i-2)+j)=0;
- end
- else
- for j=1:grid/2
- y((i-1)*grid+j)=0;
- end
- end
- end
- y=[y,x(i)];
- M=max(y);m=min(y)
- subplot(2,1,1);plot(t,y);
- axis([0,i,m-0.1,M+0.1]);
- title('單極性歸零波形');
 圖8.1單極性歸零波形 8.2單極性非歸零波形- function y = snrz(x)
- x=[0 1 1 0 0 0 1 0 0 0 1 1]
- grid=300;
- t=0:1/grid:length(x);
- for i=1:length(x);
- if (x(i)==1)
- for j=1:grid
- y((i-1)*grid+j)=1;
- end
- else
- for j=1:grid
- y((i-1)*grid+j)=0;
- end
- end
- end
- y=[y,x(i)];
- M=max(y);m=min(y)
- subplot(2,1,1);plot(t,y);
- axis([0,i,m-0.1,M+0.1]);
- title('單極性非歸零波形');
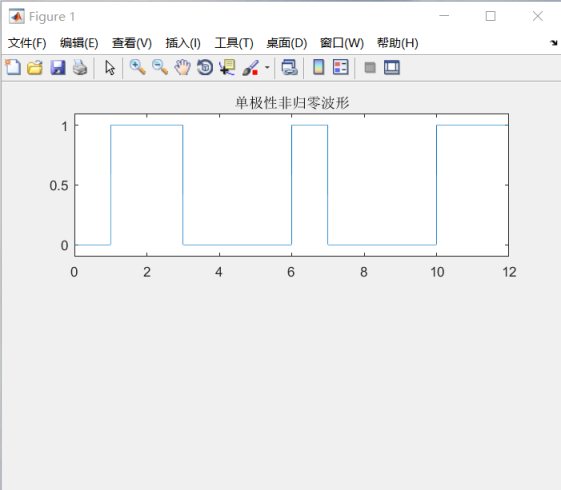
圖8.2單極性非歸零波形 8.3雙極性歸零波形- function y=drz(x)
- x=[1 1 0 1 0 0 0 1 0 1 0 0]
- grid=300;
- t=0:1/grid:length(x);%計算碼元的值
- for i=1:length(x);
- if(x(i)==1),%如果信息為1
- for j=1:grid/2,%該碼元對應的點取值1
- y(grid/2*(2*i-1)+j)=1;%定義前半周時間值為1
- y(grid/2*(2*i-2)+j)=0;%定義后半周時間值為0
- end
- else
- for j=1:grid/2,
- y(grid/2*(2*i-1)+j)=-1;%定義前半周時間值為-1
- y(grid/2*(2*i-2)+j)=0;%定義后半周時間值為0
- end
- end
- end
- y=[y,x(i)];
- M=max(y);m=min(y)
- subplot(2,1,1);plot(t,y);
- axis([0,i,m-0.1,M+0.1]);%用title函數來實現標記出各碼元對應的二元信息
- title('雙極性歸零波形');

圖8.3雙極性歸零波形 8.4雙極性非歸零波形- function y = dnrz(x)
- x=[1 1 1 0 0 1 0 0 0 0 1 0]
- grid=300;
- t=0:1/grid:length(x);
- for i=1:length(x);
- if (x(i)==1)
- for j=1:grid
- y((i-1)*grid+j)=1;
- end
- else
- for j=1:grid
- y((i-1)*grid+j)=-1;
- end
- end
- end
- y=[y,x(i)];
- M=max(y);m=min(y)
- subplot(2,1,1);plot(t,y);
- axis([0,i,m-0.1,M+0.1]);
- title('雙極性非歸零波形');
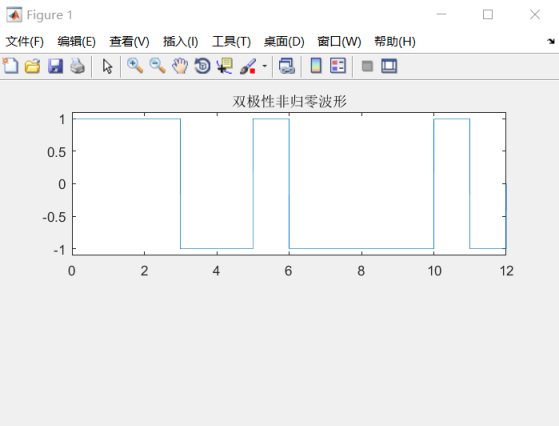
圖8.4雙極性非歸零波形 8.5AMI碼- %ami.m
- function y=ami(x)
- x=[1 1 0 1 1 0 1 1 0 0 0 0]
- %輸入x為二進制碼,輸出y為編好的碼
- t0=200;%每個碼元200個點
- t=0:1/t0:length(x);%時間序列
- p0=-1;%設定第一個碼元之前是零電平
- for i=1:length(x);%計算碼元的值
- if x(i)==1
- if p0==-1;
- for j=1:t0/2,%如果輸入信息為1,碼元對應的點的值取1
- y((2*i-2)*t0/2+j)=1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end
- p0=1;
- else
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=-1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end;
- p0=-1;
- end;
- else
- for j=1:t0
- y((i-1)*t0+j)=0;%如果輸入信息為1,碼元對應的點的值取1
- end;
- end
- end;
- N=length(y);
- temp=y(N);
- y=[y,temp];
- subplot(2,1,1);plot(t,y);
- axis([0,i,-1.1,1.1]);
- title('AMI碼');
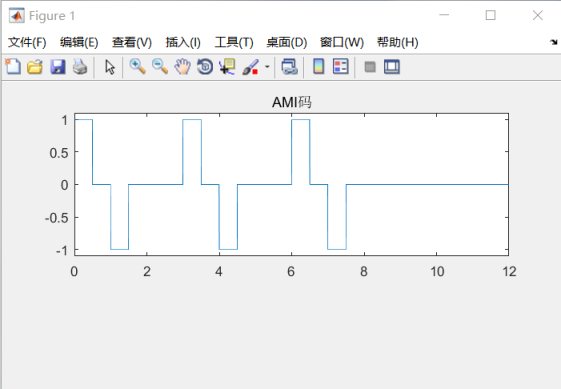
圖8.5AMI碼 8.6HDB3碼- %hdb3.m
- function y=hdb3(x)
- x=[1 1 0 1 1 0 0 1 1 0 0 1]
- %輸入x為二進制碼,輸出y為編好的碼
- t0=200;%每個碼元200個點
- t=0:1/t0:length(x);%時間序列
- zerocount=0;%該變量用于統計連零的數量
- bcount=0;%該變量用于統計上一個V脈沖以來B脈沖的數量
- B=1;%該變量存儲前一個脈沖的極性,等于1時為正脈沖,等于負1時為負脈沖
- %循環處理二進制序列
- for i=1:length(x);%計算碼元的值
- if x(i)==1 %如果為符號1
- zerocount=0;%連零統計清零
- bcount=bcount+1;%B脈沖數量+1
- if B==1;%如果前一個脈沖為正脈沖,輸出一個負脈沖
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=-1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end;
- B=-1;%更新B
- else %%如果前一個脈沖為負脈沖,輸出一個正脈沖
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end
- B=1;%更新B
- end
- else %如果為符號0
- zerocount=zerocount+1;%連零統計+1
- if zerocount==4;%如果連零數量等于4
- if mod(bcount,2)==1;%如果自上一V脈沖以來已經有奇數個B
- if B==1;%如果前一個脈沖為正脈沖,輸出一個正的V脈沖,這時取代節是000V+
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end
- else %如果前一個脈沖為負脈沖,輸出一個負的V脈沖,這時取代節是000V+
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=-1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end
- end
- else%如果自上一V脈沖以來已經有偶數個B
- if B==1%如果前一個脈沖為正脈沖,輸出一個負的V脈沖,這時取代節是B-00V-
- for j=1:t0/2%調整往前數第三個符號為B-
- y((2*i-2-6)*t0/2+j)=-1;%定義前半段時間值為1
- y((2*i-1-6)*t0/2+j)=0;%定義后半段時間值為0
- end
- B=-1%更新B
- else
- %如果前一個脈沖為負脈沖,輸出一個正的V脈沖,這時取代節是B+00V+
- for j=1:t0/2;%調整往前數第三個符號為B-
- y((2*i-2)*t0/2+j)=+1;
- y((2*i-1)*t0/2+j)=0;
- end;
- for j=1:t0/2
- y((2*i-2-6)*t0/2+j)=+1;
- y((2*i-1-6)*t0/2+j)=0;
- end
- B=+1;%更新B
- end
- end
- bcount=0;% bcount清零
- zerocount=0;% bcount清零
- else %如果不是4連零,直接輸出0
- for j=1:t0
- y((i-1)*t0+j)=0;
- end;
- end;
- end;
- end %end for
- N=length(y);
- temp=y(N);
- y=[y,temp];
- subplot(2,1,1);plot(t,y);
- axis([0,i,-1.1,1.1]);
- title('HDB3');
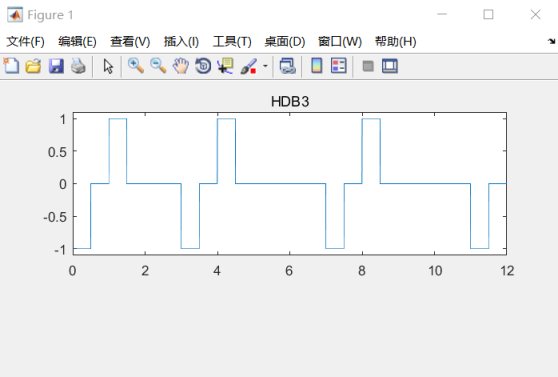 圖8.6HDB3碼 8.7曼徹斯特碼- %manchester.m
- function y=manchester(x)
- x=[1 1 0 1 0 0 1 1 0 1 0 0 1]
- %輸入x為二進制碼,輸出y為編好的碼
- t0=200;%每個碼元200個點
- t=0:1/t0:length(x);%時間序列
- for i=1:length(x);%計算碼元的值
- if x(i)==1
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=1;%定義前半段時間值為1
- y((2*i-1)*t0/2+j)=0;%定義后半段時間值為0
- end;
- else
- for j=1:t0/2
- y((2*i-2)*t0/2+j)=0;%定義前半段時間值為0
- y((2*i-1)*t0/2+j)=1;%定義后半段時間值為1
- end;
- end;
- end;
- N=length(y);
- temp=y(N);
- y=[y,temp];
- subplot(2,1,1);plot(t,y);
- axis([0,i,-0.1,1.1]);
- title('曼徹斯特碼');

圖8.7曼徹斯特碼 8.8Miller- x=[1 0 0 1 0 0 1 1];
- y=-ones(2,9);
- k=find(x==1);
- if length(k)~=0
- y(:,k(1))=[0,1]';
- flag=1;
- end
- for ii=1:length(x)
- if (x(ii)==1)&(ii==k(1))
- continue
- elseif (x(ii)==1)&(flag==0)
- y(:,ii)=[0,1]';
- flag=1;
- elseif (x(ii)==1)&(flag==1)
- y(:,ii)=[1,0]';
- flag=0;
- end
- if(x(ii)==0)&(x(ii-1)==0)&(flag==0)
- y(:,ii)=[1,1]';
- flag=1;
- elseif(x(ii)==0)&(x(ii-1)==0)&(flag==1)
- y(:,ii)=[0,0]';
- flag=0;
- elseif(x(ii)==0)&(x(ii-1)==1)&(flag==0)
- y(:,ii)=[0,0]';
- flag=0;
- elseif(x(ii)==0)&(x(ii-1)==1)&(flag==1)
- y(:,ii)=[1,1]';
- flag=1;
- end
- end
- y(:,9)=[0,0];
- milecode1=reshape(y,1,18);
- stairs(milecode1,'r');
- title('Miller');
- hold on;
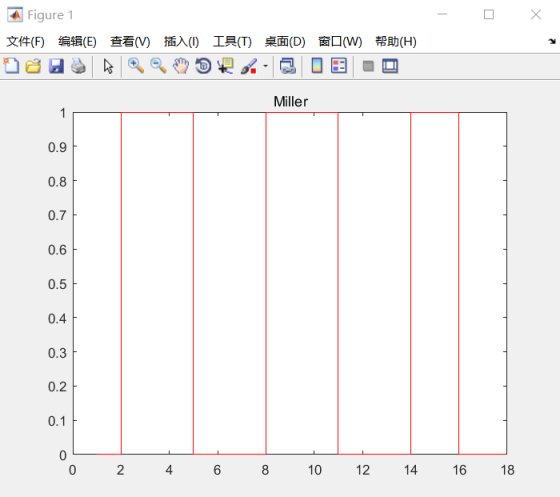
圖8.8Miller
九、心得體會經過課程設計,培養了我獨立思考的能力,增強了對通信原理這門課程的興趣。 我們在課堂上掌握的僅僅是專業基礎課的理論面,但是通過課程設計,我們就可以把所學的專業基礎理論知識用到實踐中。雖然在剛開始編程序感覺無處下手,但隨著對matlab的逐漸了解,發現matlab其實并沒有想象中的那么難。而且通過用matlab仿真基帶傳輸系統,對數字通信、數字信號處理都有更深刻的理解。 實踐出真知。這次課程設計,提高了獨立思考的能力,培養了發現問題解決問題的能力。不僅如此,我還認知到學習是一環扣一環的,之前的matlab的學習課程在這門課中也占了很重要的地位。在編寫代碼的時候,不能急于剛開始就對著電腦編寫程序,一定要理解和整理出來你所想要做什么。通過畫流程圖,可以發現在代碼編寫的過程中不僅效率高,而且成功率也高。并且在程序中過多的嵌套for循環語句和if選擇語句,很容易不小心就會導致代碼錯誤,所以程序中應盡量避免。 課程實際讓我發覺平時所學的知識有了實用的價值,達到了理論與實際相結合的目的,鍛煉了自己的能力,思路即出路,當遇見不懂不會的問題時,即使請教。只要認真鉆研,動腦思考,敢于實踐,堅持不懈,最終會取得不小的進步。
完整的Word格式文檔51黑下載地址:
 數字基帶傳輸系統.doc
(786 KB, 下載次數: 35)
數字基帶傳輸系統.doc
(786 KB, 下載次數: 35)
2018-6-13 08:49 上傳
點擊文件名下載附件
數字基帶
|