Railroad gets narrower and meets at horizon.

In Euclidean space (geometry), two parallel lines on the same plane cannot intersect, or cannot meet each other forever. It is a common sense that everyone is familiar with.

However, it is not true any more in projective space, for example, the train railroad on the side picture becomes narrower while it moves far away from eyes. Finally, the two parallel rails meet at the horizon, which is a point at infinity.

Euclidean space (or Cartesian space) describe our 2D/3D geometry so well, but they are not sufficient to handle the projective space (Actually, Euclidean geometry is a subset of projective geometry). The Cartesian coordinates of a 2D point can be expressed as (x, y).

What if this point goes far away to infinity? The point at infinity would be (∞,∞), and it becomes meaningless in Euclidean space. The parallel lines should meet at infinity in projective space, but cannot do in Euclidean space. Mathematicians have discoverd a way to solve this issue.

Homogeneous coordinates, introduced by August Ferdinand Möbius, make calculations of graphics and geometry possible in projective space. Homogeneous coordinates are a way of representing N-dimensional coordinates with N+1 numbers. （齊次坐標系是用N+1組數據表示N維坐標系的方式）

To make 2D Homogeneous coordinates, we simply add an additional variable, w, into existing coordinates. Therefore, a point in Cartesian coordinates, (X, Y) becomes (x, y, w) in Homogeneous coordinates. And X and Yin Cartesian are re-expressed with x, y and w in Homogeneous as;
X = x/w
Y = y/w

For instance, a point in Cartesian (1, 2) becomes (1, 2, 1) in Homogeneous. If a point, (1, 2), moves toward infinity, it becomes (∞,∞) in Cartesian coordinates. And it becomes (1, 2, 0) in Homogeneous coordinates, because of (1/0, 2/0) ≈ (∞,∞). Notice that we can express the point at infinity without using "∞".（w為0時，可表示無窮遠處的坐標，齊次坐標系使坐標系有了距離的概念，達到透視效果）

As mentioned before, in order to convert from Homogeneous coordinates (x, y, w) to Cartesian coordinates, we simply divide x and y by w;


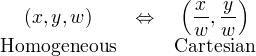
Converting Homogeneous to Cartesian, we can find an important fact. Let's see the following example;

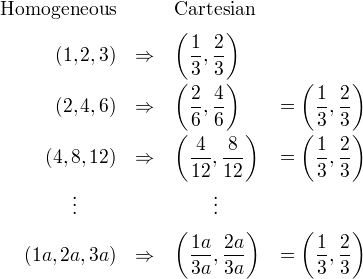
As you can see, the points (1, 2, 3), (2, 4, 6) and (4, 8, 12) correspond to the same Euclidean point (1/3, 2/3). And any scalar product（數量積）, (1a, 2a, 3a) is the same point as (1/3, 2/3) in Euclidean space. Therefore, these points are"homogeneous" because they represent the same point in Euclidean space (or Cartesian space). In other words, Homogeneous coordinates are scale invariant（縮放不變性）.

Consider the following linear system in Euclidean space;

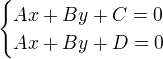
And we know that there is no solution for above equations because of C ≠ D.
If C = D, then two lines are identical (overlapped).

Let's rewrite the equations for projective space by replacing x and y to x/w, y/w respectively.

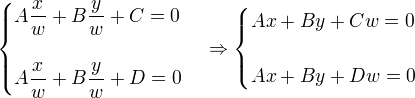
Now, we have a solution, (x, y, 0) since (C - D)w = 0, ∴ w = 0. Therefore, two parallel lines meet at (x, y, 0), which is the point at infinity. （當w為0時，C、D取任何值都能相交）

Homogeneous coordinates are very useful and fundamental concept in computer graphics, such as projecting a 3D scene onto a 2D plane.（對于在2D平面做3D場景非常有用）