懸臂角度，f為螺旋槳拉力，u電機電壓。系統的建模與仿真
3.1建模建立
電機螺旋槳懸臂構成了一組具有一定質量的機械系統，能夠在拉力的作用下，繞中心上下轉動，如圖一所示。為了簡化分析，忽略懸臂質量、忽略摩擦力。設l為懸臂長度，m電機質量，懸臂角度，f為螺旋槳拉力，u電機電壓。
圖一 受力分析
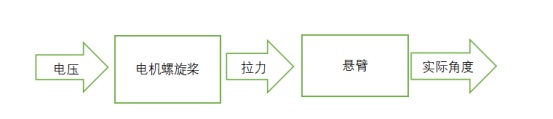
圖二 電機螺旋槳懸臂系統工作原理
角度：定義水平方向為零度，逆時針方向為正方向。
工作點：懸臂受到螺旋槳拉力和重力的共同作用。拉力與電機電壓
有關，始終垂直于懸臂與運動方向。重力在運動方向上的分量為
。若施加某個電壓
螺旋槳產生拉力
，使懸臂穩定停留在某個位置，則此時
。這時就構成了一個工作點
。
3.1.1電機螺旋槳模型
給電機施加電壓u，電機帶動螺旋槳旋轉產生拉力f，已知電機電壓和轉速的簡化數學模型為一階線性微分方程。
（1）
其中T為時間常數，表征了系統的響應速度快慢。K為系統穩態增益，表征了當轉速穩定不變時，電壓和轉速成正比。
電機電壓和轉速之間的傳遞函數由式（1）可知為
（2）
這里假設在工作點附近螺旋槳拉力和電機轉速成正比，Kf是比例系數。那么拉力和電壓的傳遞函數可以得到
（3）
3.1.2懸臂系統數學模型
切線方向上的運動方程由牛頓第二定律可得
（4）
其中，b代表摩擦阻力。方程中存在難以分析的非線性項
。但是我們可以使用微小偏差法對其在某個特定的工作點附近進行線性化。首先將力和轉角表達為工作點附近的增量形式，
，
帶入上式得到
（5）
（6）對非線性項
在工作點
處使用一階泰勒級數展開進行局部線性化
（7）將式（7）代入式（6），并考慮到 
，得到近似后的線性方程
（8）為了簡化表達，去掉△符號，并整理為標準形式
（9）傳遞函數
（10）3.1.3電機螺旋槳懸臂系統數學模型
電機螺旋槳懸臂可以看作一個整體，則合并式（3）（10）、消去中間變量F(s)，得到指令電壓和懸臂實際角度的傳遞函數為
（11）當懸臂位于水平線下方時，
，
，則
是一個正數。此時分母多項式里沒有負系數。
懸臂系統為三階系統，有3個極點
、
、
。如果電機的反應速度非常快，遠快于懸臂的反應速度，也就是說對應的極點遠離虛軸，其他兩個極點是主導極點。則可以簡化為2階系統。
（11）3.2 PID 控制以及MATLAB仿真
比例控制能夠提高系統響應速度，減小穩態誤差，但是穩定性減弱、震蕩加劇。因此引入微分控制抑制震蕩改善穩定性。如果希望消滅穩態誤差，就需要引入積分環節提高系統穩定性。
仿真圖
利用simulink中進行仿真分析查看P、PD、PI、PID控制器的控制效果
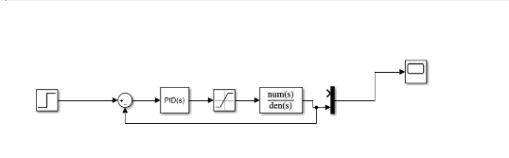
圖一 仿真原理
說明：圖一為控制系統的simulink仿真模型。
PID 控制是工業控制實踐中最常見的控制算法（95%以上）。控制器由比例單元（P， proportional）、積分單元（I，integral）和微分單元（Dderivative）組成，包含 Kp、Ki 和 Kd 三個需要設定的系數。控制原理如圖 2所示，微分方程及傳遞函數如下式所示。
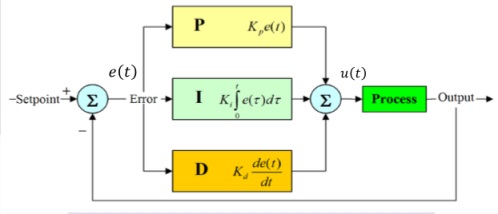
PID控制原理圖
PID 控制器的比例、積分和微分作用分別對應當前誤差、過去累計誤差及誤差變化速度（未來誤差）。若是不知道受控系統的特性，一般認為 PID 控制器是最適用的控制器。借由 調整 PID 控制器的三個參數，可以調整控制系統，設法滿足設計需求。控制器的響應可以用 控制器對誤差的反應快慢、控制器超調程度及系統震蕩的程度、穩態誤差大小來表示。 根據具體應用場合可以使用PID 控制的各種組合，如P控制、PI控制、PD控制等。其中以PI控制最常用，I 控制能夠消除穩態誤差。D 控制對反饋信號噪聲十分敏感，需要精心
設計。
比例、積分、微分算法在沒有計算機的年代是使用模擬器件來實現的。現代工業中普遍 使用數字計算機實現。計算機以固定時間間隔????不斷的重復運行 PID 控制算法，第 k 次的比 例控制項????(??)、微分控制項????(??)、積分控制項????(??)分別如下
然后 合成控制器的總輸出
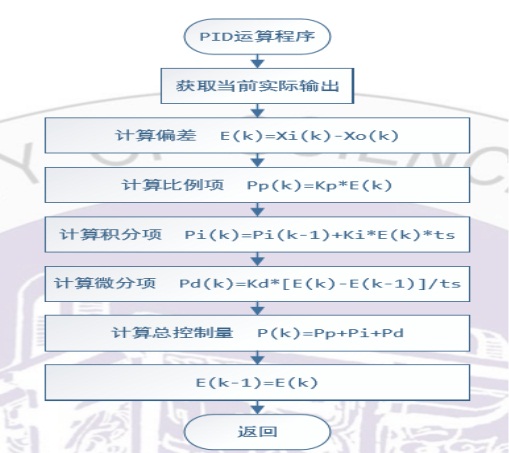
PID算法流程圖
1. 微分控制對高頻擾動十分敏感，需要設法抑制；
2. 積分控制存在積分飽和問題，對控制效果影響較大，需要解決；
4系統硬件電路設計和軟件編程
4.1電路設計
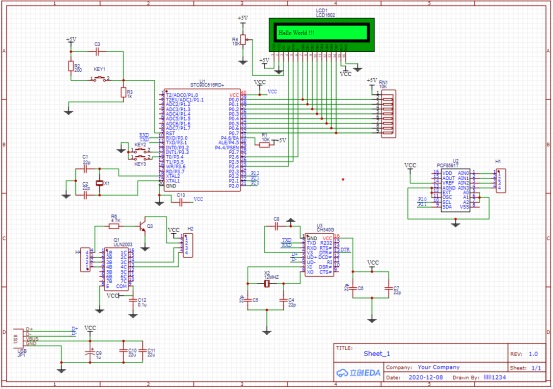
總電路圖
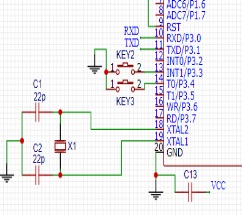
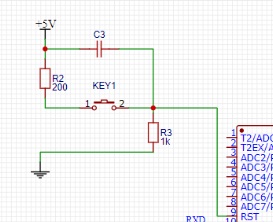
局部電路圖1（總開關） 局部電路圖2（晶振）
局部電路圖3（USB讀寫模塊）
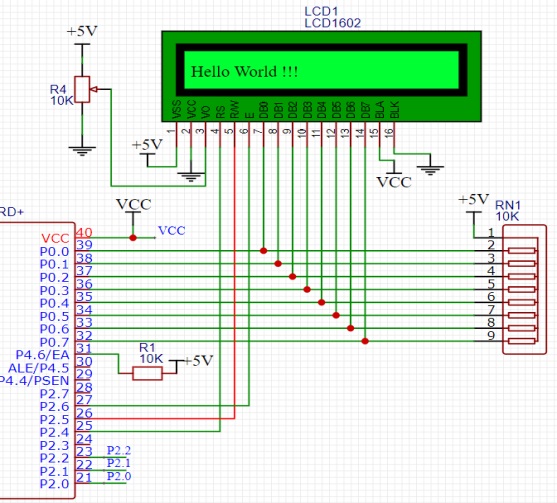
局部電路圖4（LED顯示屏模塊）
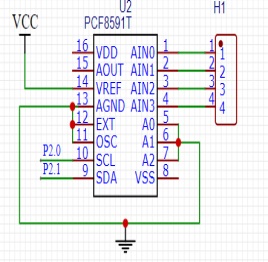
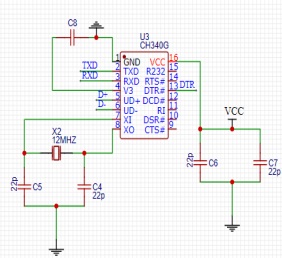
局部電路圖5（USB轉串口模塊） 局部電路圖6（ad轉換模塊）
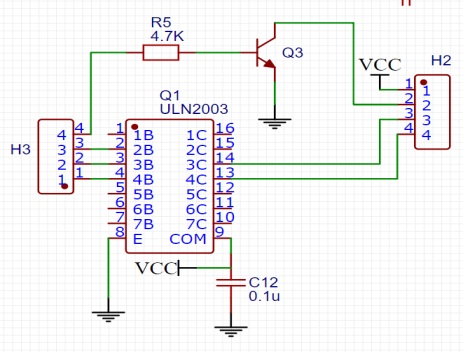
局部電路圖6（電機驅動模塊模塊）
說明：利用89C51單片機來實現對直流電機的PID控制以及實時狀態數據的顯示。
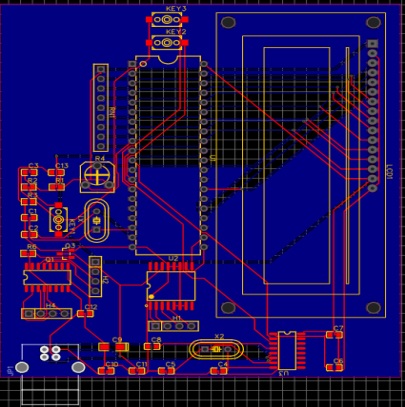4.1.3 PCB電路圖
PCB圖
PCB三維圖
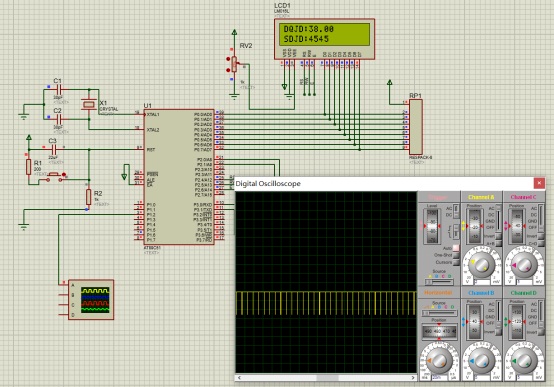
說明：仿真符合預期效果。
單片機STC90C516RD+（1）
PCF8591T ad轉換芯片——（1）
CH340G USB轉串口芯片——（1）
ULN2003電機驅動芯片——（1）
LED顯示屏LCM1602K-NSW-BBW——（1）
Micro USB連接器——（1）
開關K2-1107ST-A4SW-06——（3）
排針X6511WV-04H-C30D60——（3）
晶振X49SD27MSD2SC——（2）
三極管2n3904S-RTK/PS——（1）
電阻：10KΩ——（2）；200Ω——（1）；4.7K——（1）；10KΩ可變電阻VZ067TL1B103——（1）；10K排阻C26615——（1）
電容：10u——（1）；22p——（6）；104——（2）；0.1u——（1）22u——（2）電化學電容1u——（1）
原理圖
說明：
我們用51單片機去控制電機轉到指定角度，并通過lcd顯示出來
系統的綜合測試和評估
比例（P）控制
當控制器的輸出與偏差成比例時，稱之為比例控制（proportional control）。即 
系統閉環傳遞函數為 
利用終值定理求得單位階躍響應的穩態值
分析可知 ，電機的指令電壓控制了電機轉速，即拉力。比例控制意味著拉力和誤差成正 比。因此： 1) 比例控制必然存在誤差。誤差是產生拉力的源泉，沒有誤差就沒有拉力。要維持一 定的拉力，????越大，所需的誤差就越小； 2) 比例控制器的輸出只和誤差成正比，????越大，控制器反應越靈敏。當懸臂快速沖到 指定位置時，誤差為 0，拉力也為 0，加速度為 0。雖然懸臂的加速度為 0，但可能 還會存在一定速度，產生過沖。
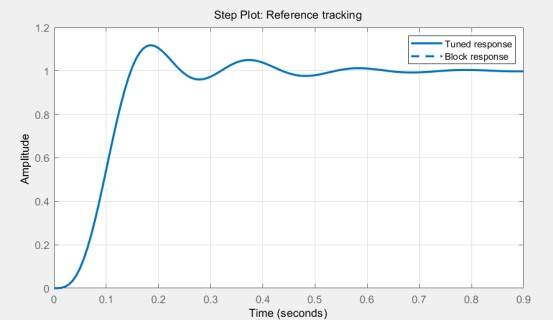
圖一P控制的理論曲線
通過實驗我們發現Kp較大時會加快響應速度快速達到穩定，能減少誤差但不能消除誤差，Kp越大時會很容易引起振蕩；Kp減小，發生振蕩的可能性減小，但調節速度變慢。
比例微分（PD）控制
一個控制系統的基本要求是穩定、準確、快速。增加比例控制系數能夠減小偏差提高準 確性、減小反應時間提高快速性。但是同時帶來的問題就是系統穩定性減弱，表現為容易過 沖、產生震蕩。 當控制器輸出不僅和偏差成比例，同時還與偏差的變化速度（微分）成比例時，稱之為 比例微分控制（Proportional + Derivative control）。
即： 
對應傳遞函數：
PD控制中的比例項能夠減小偏差，微分項能夠減小偏差的變化速度、抑制振蕩。PD控制方框圖如下圖所示。
如果懸臂能夠簡化為標準二階系統
，則 PD 控制的閉環傳遞函數為
從理論上分析，增加 Kd會增加阻尼比，抑制振蕩。單純的比例控制器增加Kp 能夠減小誤差、增加響應速度，但是會增加超調、惡化穩定性。產生超調的原因前面已經簡要說明過，原因是當偏差為0時，偏差的速度不為0，這時引入微分控制作用可以抑制偏差的變化。理想情況是偏差為0時，偏差的速度也為 0，達到穩定狀態。
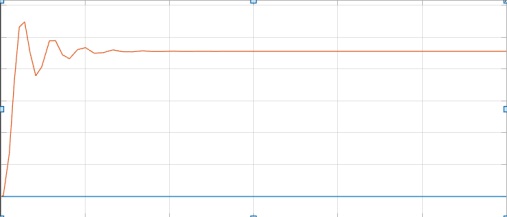
圖五pd控制理論響應曲線
經過調節我們發現理論和實際有一些不吻合我們認為是在現實系統中系統響應速度慢，使微分環節作用削弱。微分控制可以改善動態特性,如超調量減少,調節時間縮短,允許加大比例控制,使靜差減小,提高控制精度。但當Kd偏大或偏小時,超調量較大,調節時間較長,只有合話的時候,才可以得到比較滿意的過渡過程。
比例積分（PI）控制
在積分控制中，控制器的輸出與輸入誤差信號的積分成正比關系。對一個自動控制系統，如果在進入穩態后存在穩態誤差，則稱這個控制系統是有穩態誤差的或簡稱有差系統（System with Steady-state Error）。為了消除穩態誤差，在控制器中必須引入“積分項”。積分項對誤差取決于時間的積分，隨著時間的增加，積分項會增大。這樣，即便誤差很小，積分項也會隨著時間的增加而加大，它推動控制器的輸出增大使穩態誤差進一步減小，直到等于零。因此，比例+積分(PI)控制器，可以使系統在進入穩態后無穩態誤差。積分調節作用：是使系統消除穩態誤差,提高無差度。因為有誤差,積分調節就進行,直至無差,積分調節停止,積分調節輸出一常值。積分作用的強弱取決與積分時間常數Ti, Ti越小,積分作用就越強。反之Ti大則積分作用弱,加入積分調節可使系統穩定性下降,動態響應變慢。積分作用常與另兩種調節規律結合,組成PI調節器。
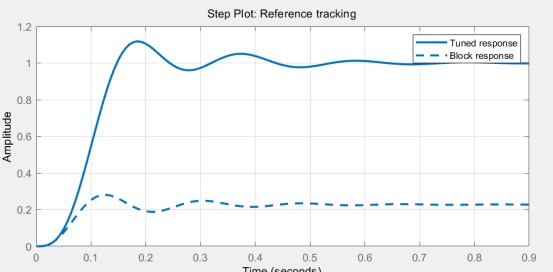
圖九 kp0.018 ki0.58理論響應曲線
從圖中對比可以發現積分環節的作用是：只要系統存在誤差，積分控制作用就不斷地積累，輸出控制量以消除誤差。因此只要有足夠的時間，積分控制將能完全消除誤差，但是積分作用太強會使系統超調加大，甚至使系統出現振蕩。
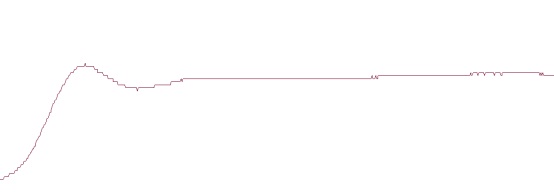
圖二 kp=0.5 ki=0.6 kd=0.15響應曲線
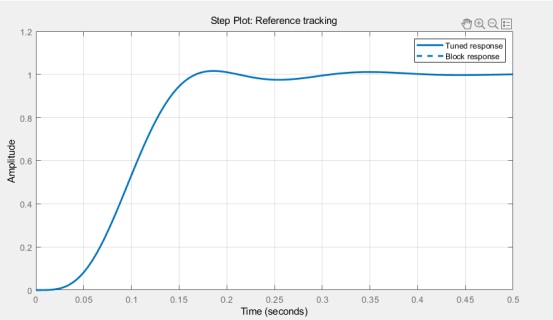
圖三 kp=0.5 ki=0.6 kd=0.15響應曲線理論響應曲線
我們發現PID控制可以較好地實現系統穩定通過PID算法的組合可有效地糾正被控制對象的偏差，從而使其達到一個穩定的狀態。但實際系統和理論系統總存在不足無法達到想要的理論狀態，我們在實際中發現該組pid可以很好的控制懸臂系統因此選用該組pid參數。
在這次設計中我們首先將項目分成三部分：第一部分通過51單片機將角度讀出，第二部分實現按鍵能改變設定角度，第三部分實現可以通過pid控制螺旋槳懸停在特定角度。
在實現項目過程中我們遇到了一些困難，并通過組員的一起努力解決問題。
（1）在讀取電位器角度并將其顯示在LCD上時，我們發現電位器讀到的數據并不能及時顯示在LCD上，有很長的延時。我們通過查閱資料和咨詢老師最終發現在我們的庫函數里存在較長時間延時從而導致數據不能被及時顯示，我們刪去了延時，發現角度可以很好顯示在LCD上。
（2）在調試程序時我們發現讀取的角度和設定的角度并不能一起顯示在LCD上，我們把自己所寫的顯示函數封裝成函數，并將顯示當前角度的代碼放在設定角度代碼上面，通過這樣的調試我們的LCD可以很好顯示。
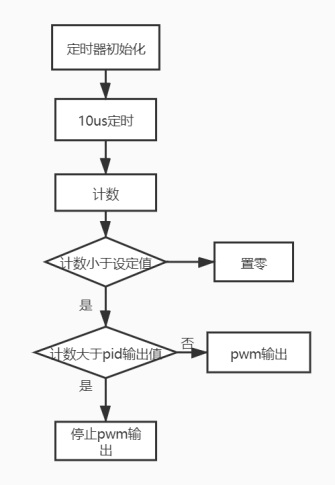
（3）在pid控制時我們發現單片機雖然可以實現對電機控制但是波動周期和時間都很大，經過查閱資料和討論我們發現應該是定時器中斷時間和pwm周期存在問題，經過試驗我們把定時器中斷時間設置在10微秒，pwm周期為1毫秒，
這時的電機可以很好的控制。
（4）在調試過程中我們發現螺旋槳雖然可以轉到指定角度但是只會維持一定的時間并不能長時間維持在指定角度，我們經過討論，和查閱資料認為是pid的計算存在問題，我們重新設計了pid的計算方法，最終解決了這些問題。
在整個系統調試過程中我們
（5）比例控制一定存在誤差。誤差是產生拉力的源泉，沒有誤差就沒有拉力。比例控制器的輸出只和誤差成正比，比例控制當快速到指定位置時，會發生過沖。
用比例微分控制時，PD控制中的比例項能夠減小偏差，微分項能夠減小偏差的變化速度、抑制振蕩。微分控制可以改善動態特性,如超調量減少,調節時間縮短,允許加大比例控制,使靜差減小,提高控制精度。但當Kd偏大或偏小時,超調量較大,調節時間較長,只有合話的時候,才可以得到比較滿意的過渡過程。
比例+積分(PI)控制器，積分環節可以使系統在進入穩態后無穩態誤差，提高誤差度。
PID控制可以較好地實現系統穩定通過PID算法的組合可有效地糾正被控制對象的偏差，從而使其達到一個穩定的狀態。
（6）電路圖的繪制起初對整體電路圖不熟悉，導致在Proteus中仿真失敗，后來發現是硬件型號不對，不同型號和規格的電容以及三極管對電路的影響會累積，導致最后的結果誤差極大，最后在多次更換調試后得以解決。
（7）PCB板的繪制最開始在AD上繪制，但各種元件庫還需要下載極其不方便，導致浪費了很多時間，究其原因也是對軟件的不熟悉，之后用的eda在線繪圖，進度就加快了很多，對應的元器件也能看見實物圖以及對應封裝，能夠對元件有更深刻的印象。
| 歡迎光臨 (http://m.raoushi.com/bbs/) | Powered by Discuz! X3.1 |