��(bi��o)�}: ���F(xi��n)��������Փ����ԇԇ�� ���ܴ���������? [��ӡ���]
����: izhineng �r(sh��)�g: 2017-12-28 02:32
��(bi��o)�}: ���F(xi��n)��������Փ����ԇԇ�� ���ܴ���������?
���F(xi��n)��������Փ��ԇ��
1. �\������(zh��n)��(sh��)�W(xu��)ģ���c���ѿ���Ҏ(gu��)�ɵ����ü������g���P(gu��n)ϵ��
�����Ԅ�(d��ng)���Ƶ�ϵ�y(t��ng)�У�����ʹ�҂��O(sh��)Ӌ(j��)���Ԅ�(d��ng)����ϵ�y(t��ng)�ķ�(w��n)���Ժ͕��B(t��i)���ܝM���҂���Ҫ���҂��ͱ��Ҫ��ϵ�y(t��ng)�ĕ��B(t��i)�^���M(j��n)�ж�������Փ���������������(n��i)�ڵĿ���Ҏ(gu��)�ɡ�
�Á�����ϵ�y(t��ng)������֮�g����P(gu��n)ϵ�Ĕ�(sh��)�W(xu��)���_(d��)ʽ����ϵ�y(t��ng)�Ĕ�(sh��)�W(xu��)ģ�ͣ����������������������Ԍ�һ��(g��)���w��ϵ�y(t��ng)����(j��)���(n��i)���Y(ji��)��(g��u)�D(zhu��n)׃���҂���Ϥ�Ĕ�(sh��)�W(xu��)���_(d��)ʽ����Փ�dž�ݔ���ݔ��ϵ�y(t��ng)���ַ��̡����f����(sh��)߀�Ƕ�ݔ���ݔ���µĠ�B(t��i)���̡�
��ϵ�y(t��ng)�Ŀ���Ҏ(gu��)�ɣ����Ծ��w�����緀(w��n)�B(t��i)�`��{(di��o)��(ji��)�r(sh��)�g�����{(di��o)�����ɿ��Ե��@Щָ��(bi��o)��ͨ�^�@Щָ��(bi��o)���Զ���������ϵ�y(t��ng)�������_��(d��ng)�����ܲ��ܰ����҂���Ҫ���M(j��n)�п��ƣ����Ƶ�Ч����Ρ�
ÿһ��(g��)�_���Ŀ���ϵ�y(t��ng)�������г���Ψһ�Ķ���(g��)��(sh��)�W(xu��)ģ�ͣ��ڲ�ͬ�Ĕ�(sh��)�W(xu��)ģ�����҂���ϵ�y(t��ng)����Ҏ(gu��)�ɷ����Ă�(c��)���c(di��n)���M��ͬ���������о�ϵ�y(t��ng)�ɿ��ԕr(sh��)�����һ�_ʼ��ģ�҂��͜�(zh��n)�_���г������(bi��o)��(zh��n)�ԣ��@�͌��҂�֮��ķ��������˷���Ϳ�ݡ����Ҳ�ͬ��͵Ŀ���ϵ�y(t��ng)Ҳ���������m�õ�ģ�ͣ��ڶ�ݔ���ݔ����ϵ�y(t��ng)���҂�?n��i)��߀������̖(h��o)���D���߂��f����(sh��)��ģ�ͣ���ô������ģ���y߀���ܕ�(hu��)��ϵ�y(t��ng)Ҏ(gu��)�ɵķ������F(xi��n)�^���ƫ��C������������(zh��n)�Ĕ�(sh��)�W(xu��)ģ�Ϳ��Ԝ�(zh��n)�_����������ϵ�y(t��ng)������Ҏ(gu��)�ɣ�ͨ�^��ģ�͵ķ����҂����Ԝ�(zh��n)�_���լF(xi��n)�еĿ���Ҏ(gu��)�ɣ��Ķ�����(j��)��Ҫ��ϵ�y(t��ng)�M(j��n)�и��ƣ�ʹϵ�y(t��ng)���õ���ɿ���Ҫ��
2. �������殐����׃�Q�ڿ���ϵ�y(t��ng)�����е����ã�
����һ��(g��)�_���Ŀ���ϵ�y(t��ng)�У��҂������x��ͬ�Ġ�B(t��i)׃���Ͳ�ͬ����ʽ���M(j��n)������������ͬһ��(g��)����ϵ�y(t��ng)���Ԍ�����ͬ�ľ�ꇣ����殐����׃�Q���nj�ԭ��B(t��i)ʸ��������׃�Q���Ķ��ó���һ��B(t��i)ʸ������ϵ�y(t��ng)�Ġ�B(t��i)���g���_(d��)ʽ׃���µ���ʽ�����殐����׃�Qֻ�nj�����ϵ�y(t��ng)�ķ���׃���ˣ�ϵ�y(t��ng)������ֵ��ϵ�y(t��ng)�������]��׃������Ӱ��䷀(w��n)���ԡ��ܿ����^�ԡ����殐����׃�Q������ϵ�y(t��ng)�ķ���׃��һ�N�����҂���ֱ�^����ϵ�y(t��ng)����ʽ�����猦�ǘ�(bi��o)��(zh��n)�Ϳ����҂�ֱ�^�õ�ϵ�y(t��ng)�ķ�(w��n)���ԣ������ؘܿ�(bi��o)��(zh��n)�ͺ����^��(bi��o)��(zh��n)�̈́t�����҂����õķ������ܿغ����^�ԡ�
3.�\����B(t��i)�����c��B(t��i)�^�y���ژO�c(di��n)���Õr(sh��)�ķ��x���ԣ�
�����S�����ϵ�y(t��ng)�У��҂���(sh��)�F(xi��n)����Ȇ��}�r(sh��)��Ҫ��Ҫ��B(t��i)�����������S���B(t��i)׃���o��ֱ�әz�y������B(t��i)�^�y�����Ԍ�(sh��)�F(xi��n)��B(t��i)�������������]�h(hu��n)ϵ�y(t��ng)�У��O�c(di��n)����ֱ�Ӡ�B(t��i)����ϵ�y(t��ng)�ĘO�c(di��n)���^�y�������ĘO�c(di��n)�ɂ�(g��)���֣������@���ߪ�(d��)��������x�����^�y����(g��u)�ɵķ����]�h(hu��n)ϵ�y(t��ng)��ֻҪϵ�y(t��ng)�܉��^�y�����B(t��i)������ꇺ��^�y�������e�C���Ӱ푣����֪�(d��)�������Էքe�O(sh��)Ӌ(j��)���@��(g��)���|(zh��)�Q���]�h(hu��n)�O�c(di��n)�O(sh��)Ӌ(j��)�ķ��x�ԡ�
4. ʲô�ǽ�����ƣ� ������һ���ȡʲô������
���ڶ�ݔ���ݔ���Ŀ���ϵ�y(t��ng)�У�ÿ��(g��)ݔ��֮�g����ã�ÿ��(g��)ݔ�����յ�����(g��)ݔ��Ŀ��ƣ��@�o�҂���ϵ�y(t��ng)�ķ�������˺ܴ����y��������ƾ���ʹϵ�y(t��ng)�е�ÿһ��(g��)ݔ����ֻ�܆�(g��)ݔ��Ŀ��ơ��ڹ�����һ���Ѓ��з�����ǰ���a(b��)��������͠�B(t��i)�������
- ��������ϵ�y(t��ng)��(w��n)���Ե���ҪӰ����ؼ������ж�������
�𣺮�(d��ng)�_��(d��ng)���Õr(sh��)��ݔ������ƫ�xԭ���ķ�(w��n)��ֵ���@�r(sh��)���ڷ���������ͨ�^ϵ�y(t��ng)��(n��i)�����Ԅ�(d��ng)�{(di��o)��(ji��)��ϵ�y(t��ng)���Իص�ԭ���ķ�(w��n)��ֵ��(w��n)�������˕r(sh��)ϵ�y(t��ng)ʹ��(w��n)���ģ���(d��ng)ϵ�y(t��ng)��һ��(g��)��(w��n)�B(t��i)�^�ȵ���һ��(g��)��(w��n)�B(t��i)�r(sh��)����Ҫ��(j��ng)�vһ��(g��)�^���^�̣������@��(g��)�^���^�����ܵ�ָ��(bi��o)�������B(t��i)����ָ��(bi��o)���������{(di��o)���������r(sh��)�g���{(di��o)��(ji��)�r(sh��)�g����ʎ�Δ�(sh��)�ȡ��ڌ�(sh��)�H������ֻ���ж���(w��n)��߀�����҂�߀Ҫ֪��ϵ�y(t��ng)�����жව(w��n)�����˕r(sh��)�҂����]ϵ�y(t��ng)�ķ�(w��n)��ԣ���Ƕ��١�
��(d��ng)���ڃ�(n��i)��������ã�ʹϵ�y(t��ng)���F(xi��n)�l(f��)ɢ��̎�ڲ���(w��n)���Ġ�B(t��i)���@�r(sh��)ϵ�y(t��ng)�Dz���(w��n)���ġ������κο���ϵ�y(t��ng)���f����Ҫ�ėl������ϵ�y(t��ng)�܉�(w��n)����
- �����B�m(x��)ϵ�y(t��ng)���䷀(w��n)����ֻȡ�Q��ϵ�y(t��ng)�����Ĺ������ԣ�ϵ�y(t��ng)�Y(ji��)��(g��u)�����ǽY(ji��)��(g��u)����(sh��)�ȣ��͔_��(d��ng)����ݔ�����]���P(gu��n)ϵ����ȡ�Q�ڔ_��(d��ng)��ʧ�B(t��i)�����Ƿ��(hu��)˥�p������ȫ�Q����ϵ�y(t��ng)�]�h(hu��n)���f����(sh��)�ĘO�c(di��n)�ֲ��������еĘO�c(di��n)����s�S��ؓ(f��)��ƽ��tϵ�y(t��ng)��(w��n)���������������Q��ϵ�y(t��ng)�ķ�(w��n)���ԣ��]�h(hu��n)��O�c(di��n)�Q��ϵ�y(t��ng)��Ʒ�|(zh��)
1����һ��(g��)��(w��n)���Г�(j��)���r(sh��)���µķ�(w��n)���Г�(j��)���m���ڵ��Aϵ�y(t��ng)��������(sh��)��(w��n)���Г�(j��)����˹��(w��n)���Г�(j��)���ՠ��SƝ�Г�(j��)�ȡ�����ԭ��߀��������ֵ��ȡֵ���Дࡣ�Ԅ�˹�Г�(j��)��������(d��ng)�г���˹������(j��)���еķ�̖(h��o)�����Д��䷀(w��n)���ԣ��ڴ_����(w��n)ԣ�ȕr(sh��)���Ԍ�ԭ�]�h(hu��n)�����е�sʹ��s=z-�Ĵ�������(w��n)�c(di��n)ԣ�Ȧġ�
2���ڶ���(g��)��(w��n)���Г�(j��)���m���ڸ��Aϵ�y(t��ng)���д�������(sh��)��ϵ�y(t��ng)������܉�E������܉�E����sƽ�����������������B�����ڈD�п��Կ��������������ķֲ�����ϵ�y(t��ng)�Ă��f����(sh��)����δ֪�ą���(sh��)K�r(sh��)���҂����Ը���(j��)��܉�E���L��Ҏ(gu��)�t������(d��ng)����Kֵ�µ���������ֵ�ķֲ���ÿ�_��һ��(g��)Kֵ���Ϳ��Եȵ�ϵ�y(t��ng)��һ�M����ֵ���Ķ�����(j��)����ֵ����sƽ��ķֲ��Д�ϵ�y(t��ng)�Ƿ�(w��n)����
3��������(g��)��(w��n)���Г�(j��)���l�������µķ�(w��n)���Г�(j��)������ʽ��(w��n)���Г�(j��)�����D����(sh��)��(w��n)���Г�(j��)����ʽ��(w��n)���Г�(j��)�nj�sƽ��ӳ�䵽��(f��)ƽ���ϡ���ʽ�����@��-1��j0���c(di��n)��r(sh��)����D(zhu��n)���ܔ�(sh��)N����sƽ���ϵ��_�h(hu��n)�O�c(di��n)��(g��)��(sh��)P���]�h(hu��n)�O�c(di��n)��(g��)��(sh��)Z���M��Z=P-N���tϵ�y(t��ng)�Ƿ�(w��n)���ġ����l��������λԣ�Ⱥ�����ԣ�ȁ��Д���������(w��n)���ԡ�
�ڲ��D����(sh��)��(w��n)���Г�(j��)���������؈D�����ֱ�^�Ŀ���ϵ�y(t��ng)�Ƿ�(w��n)���ͷ�(w��n)��ԣ�ȵĴ�С��
4�����Ă�(g��)�Г�(j��)�������ڶ�ݔ���ݔ������ϵ�y(t��ng)�����������Z��(w��n)���Г�(j��)���c��(j��ng)����Ʋ�ͬ���������Z�����x�µķ�(w��n)�������Ă�(g��)���棺��(w��n)�����u����(w��n)�������u����(w��n)���Ͳ���(w��n)�����������Z���һ�����g�ӷ����@��ͨ�^��B(t��i)���̽���������Д�ġ��䷀(w��n)���ij�Ҫ�l���Ǡ�B(t��i)���̵�����ֵС�ڵ����㡣���ڶ����t��ͨ�^��(g��u)�����Ϻ���(sh��)���ж��ġ�һ����r��ݔ���ݔ������ϵ�y(t��ng)���Г�(j��)�^�����Ҳ�ܷ����ݣ�ֻ���ڶ�ݔ���ݔ���ĕr(sh��)�������Г�(j��)�õ��^�࣬�����Г�(j��)�����ă�(y��u)���w�F(xi��n)�ڷǾ���ϵ�y(t��ng)���ж��С�
- �����xɢϵ�y(t��ng)����(d��ng)����ϵ�y(t��ng)�е���̖(h��o)�H���x���xɢ�r(sh��)�g�ϣ��@�ӵ�ϵ�y(t��ng)�Q�龀��ϵ�y(t��ng)������B�m(x��)ϵ�y(t��ng)��������֮̎���҂�ʹ��z׃�Q��������䷀(w��n)���ԡ�
1����һ��(g��)�Г�(j��)����sƽ��ӳ�䵽zƽ���ϣ�ֻҪϵ�y(t��ng)������ֵ��zƽ��Ć�λ�A��(n��i)��ϵ�y(t��ng)��(w��n)����ʹ�Ô�(sh��)�W(xu��)�P(gu��n)ϵ��z׃�Q����ʽ׃�Q�D(zhu��n)�Q֮�����(sh��)��(w��n)���Г�(j��)ͬ���m�á�
2���ڶ���(g��)�Г�(j��)����ʽ��(w��n)���Г�(j��)�����D��һ����r�²��D�õ��^��
- �Ǿ���ϵ�y(t��ng)��ԓϵ�y(t��ng)�ķ�(w��n)���Բ����Q����ϵ�y(t��ng)������������߀ȡ�Q�ڔ_��(d��ng)����ݔ������һ������Ǿ���ϵ�y(t��ng)�Ĺ��̷����ЃɷN��һ����ƽ�淨���m��һ���A��������������(sh��)�����m�ϸ��A��
1����һ��(g��)�Г�(j��)����ƽ�淨�����ؓ(f��)��������(sh��)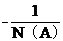 ����(d��ng)ϵ�y(t��ng)���Բ��ֵķ���������������ԓ����(sh��)�tϵ�y(t��ng)����(w��n)�����������tϵ�y(t��ng)��(w��n)����
����(d��ng)ϵ�y(t��ng)���Բ��ֵķ���������������ԓ����(sh��)�tϵ�y(t��ng)����(w��n)�����������tϵ�y(t��ng)��(w��n)���� 2���ڶ���(g��)�Г�(j��)���������Z���Г�(j��)���ڷǾ���ϵ�y(t��ng)�з�(w��n)����������ϵ�y(t��ng)��ƽ��B(t��i)���Եģ���ͬ��ƽ��B(t��i)������ͬ�ķ�(w��n)���ԣ�����ֻ�ܷքeӑՓ����(g��)ƽ��B(t��i)�����ķ�(w��n)���ԡ������н�B�������Г�(j��)�Ļ���������
���ϵ�һ���У��ڷǾ���ϵ�y(t��ng)�У�����(j��)���B(t��i)���̿��������������(sh��)���ſ˱Ⱦ�ꇣ��ٌ��侀�Ի����˕r(sh��)�õ��ľ��Ի����̵�����ֵ�Ϳ�������ϵ�y(t��ng)һ���ж����С��С�ڵ�����r(sh��)ϵ�y(t��ng)�Ƿ�(w��n)���ġ�
���ϵڶ����У��������Z���������̓��(g��u)һ��(g��)��������(sh��)��������Q���������Z��(sh��)����һ�����c����(g��)��B(t��i)׃��x��t���P(gu��n)��ӛ��V��x��t���������@��t���tӛ��V��x��������һ��(g��)��(bi��o)������(sh��)�����]����������(sh��)���Ǵ����㣬�ʞ���������(sh��)������˥�p������),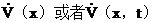 ��ʾ���������Z��ڶ�������V��
��ʾ���������Z��ڶ�������V��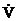 �ķ�̖(h��o)������ֱ�ӌ�ƽ���B(t��i)��(w��n)���������Д࣬�o�����ϵ�y(t��ng)��̡����w���£��O(sh��)ϵ�y(t��ng)�Ġ�B(t��i)���̞�
�ķ�̖(h��o)������ֱ�ӌ�ƽ���B(t��i)��(w��n)���������Д࣬�o�����ϵ�y(t��ng)��̡����w���£��O(sh��)ϵ�y(t��ng)�Ġ�B(t��i)���̞�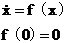 ���������һ��(g��)��(bi��o)������(sh��))V��x�������B�m(x��)��һ�Aƫ��(d��o)��(sh��)�����ҝM�㣺��1��
���������һ��(g��)��(bi��o)������(sh��))V��x�������B�m(x��)��һ�Aƫ��(d��o)��(sh��)�����ҝM�㣺��1�� V��x���������ģ���2��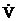 ��ؓ(f��)���ģ��tϵ�y(t��ng)��ԭ�c(di��n)̎��ƽ���B(t��i)�ǝu����(w��n)���ġ�
��ؓ(f��)���ģ��tϵ�y(t��ng)��ԭ�c(di��n)̎��ƽ���B(t��i)�ǝu����(w��n)���ġ� ���F(xi��n)��������Փ��ԇ��
- Ӌ(j��)���}��ÿ�}10�֣���50�֣�

1.ϵ�y(t��ng)�Ġ�B(t��i)���g���_(d��)ʽ��
�⣺
��matlab�ɵã�
A=[0 1;-2 -3];
>> [v,d]=eig(A)
v =
0.7071 -0.4472
-0.7071 0.8944
d =
-1 0
0 -2
������ֵ��-1��-2������������v��ꇵăɂ�(g��)��������������������
- �C����ϵ�y(t��ng)��(j��ng)����׃�Q��������ֵ��׃��
�C����
ϵ�y(t��ng)�����������ǣ�
ϵ�y(t��ng)��(j��ng)�^���殐׃�Q��
�����������ǣ�
- ���錦�Ǿ���(bi��o)��(zh��n)�͡�
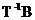 ��matlab�ɵã�
��matlab�ɵã�T=[2.8284 1.4142;2.2361 2.2361];
B=[1;1];
T*B
ans =
4.2426
4.4722
CT��matlab�ɵã�
C*v
ans =
0.7071 -0.4472

2.��֪ϵ�y(t��ng)
ԇ����ݔ���ܿ��Ժ͠�B(t��i)�ܿ��ԡ�
�⣺
��B(t��i)�ܿأ�
��matlab��֪��
a=[-4 5;1 0];
b=[-5;1];
c=[1 -1];
M=ctrb(a,b)
M =
-5 25
1 -5
��֪M��ꇲ��M�ȣ�����ԓϵ�y(t��ng)��B(t��i)���ܿء�
ݔ���ܿأ�
Rank��cb cab��=rank[-6 30]=1
ԓ��ꇝM�ȣ�����ԓϵ�y(t��ng)ݔ���ܿ�

3. ��ϵ�y(t��ng)�Ġ�B(t��i)���g���_(d��)ʽ�� ԓϵ�y(t��ng)�Ƿ����^�y�������^�y��ԇ������^�y��(bi��o)��(zh��n)�͡�
�⣺
��matlab��֪��
a=[1 -1;0 2];
b=0;
c=[-1 -0.5];
N=obsv(a,c)
N =
-1.0000 -0.5000
-1.0000 0
ԓ�Єe��ꇝM�ȣ�����ԓϵ�y(t��ng)���^�y��
�����^��(bi��o)��(zh��n)���ǣ�
4. ϵ�y(t��ng)���à�B(t��i)����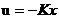 ���M���O�c(di��n)������
���M���O�c(di��n)������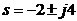 ��
��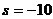 ��ģ������:
��ģ������: ԇ�����N��ͬ�����_����B(t��i)����������K��
�⣺
����һ��ԓ��ʽ�ѽ�(j��ng)���ؘܿ�(bi��o)��(zh��n)�ͣ������B(t��i)����ꇺ���������(xi��ng)ʽ���������������(xi��ng)ʽ�ǣ�
���տɵ�k=[199 55 8]
��������
���� 
�ɵã� K=[199 55 8]
��������
���������������ǣ�
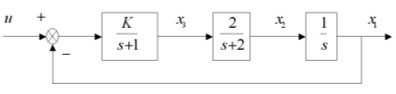
5. ԇ�_���Dʾϵ�y(t��ng)������K�ķ�(w��n)����������(y��ng)�����ϵڶ�������
�⣺��ϵ�y(t��ng)��D�ɵ����B(t��i)���̣�
�t��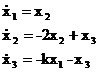 ��ԓʽ����֪����0��0���c(di��n)��ƽ���B(t��i)
��ԓʽ����֪����0��0���c(di��n)��ƽ���B(t��i) �O(sh��)���������
��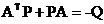 �����Ƴ�
�����Ƴ�
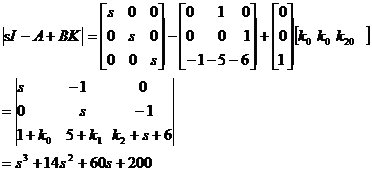
��� ��p��������ꇄt��һ�A�����A�����A����
��p��������ꇄt��һ�A�����A�����A����
ʽ��Ҫ�����㼴�� 
�ⲻ��ʽ�M����֪��k>0��12-2k>0������֪��k��ȡֵ������0<k<6
������Word��ʽ�ęn51�����d��ַ��
 ���F(xi��n)��������Փ��ԇ��.doc
(186.34 KB, ���d��(sh��): 11)
���F(xi��n)��������Փ��ԇ��.doc
(186.34 KB, ���d��(sh��): 11)
2017-12-28 02:31 �ς�
�c(di��n)���ļ������d����
���d�e��: �ڎ� -5
| �gӭ���R (http://m.raoushi.com/bbs/) |
Powered by Discuz! X3.1 |

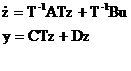




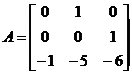 ��
�� 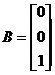
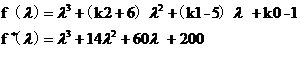
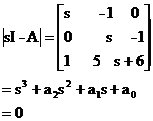
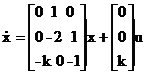
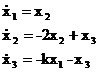 ��ԓʽ����֪����0��0���c(di��n)��ƽ���B(t��i)
��ԓʽ����֪����0��0���c(di��n)��ƽ���B(t��i)

 ��p��������ꇄt��һ�A�����A�����A����
��p��������ꇄt��һ�A�����A�����A���� 
 ���F(xi��n)��������Փ��ԇ��.doc
(186.34 KB, ���d��(sh��): 11)
���F(xi��n)��������Փ��ԇ��.doc
(186.34 KB, ���d��(sh��): 11)